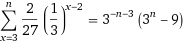It is time for social media distancing

While SARS-CoV-2 spreads across the globe with each case going on to infect between 1.4 and 3.8 other individuals[i], another viral infection first observed in Belgium[ii] is spreading with an R0 many orders of magnitude greater – with some going on to infect millions of others.

The conspiracy theory baselessly connecting the rollout of the 5G network with SARS-CoV-2 first appeared at the end of January and now yields half a billion Google search results for “5G coronavirus”, countless retweets, shares, and likes across social media platforms, and 1.3 million YouTube results some having views in the millions. Traditional media too are now presenting the theory as at least borderline credible[iii], and many mobile phone masts have been vandalized, often not yet 5G-enabled, damaging the ability of people including key-workers to stay connected during the lockdown. A “Rapid Response Unit” has been established to identify and counter misleading claims as part of the Department for Digital Culture, Media and Sport’s Counter Disinformation Cell[iv] - analysing how such misinformation is spreading - and people are being asked to only share material known to be credible.

None of this is new. Since The Selfish Gene in 1976, the idea of virally replicating ideas has been widely known, with “to go viral” being added to the Oxford English Dictionary fifteen years ago[v]. Similarly social media platforms such as Facebook and Twitter and other platforms with social sharing capability such as YouTube have been wrestling with both whether and how to address the runaway spread of misinformation and the polarization of extreme views and groups for a long time, and they are agonizingly familiar with the practical and ethical dilemmas that this yields. Whether or not the platforms or the users are responsible for content, identifying “fake news” would need to begin with a tight and non-partisan definition – already enormously problematic – and either considerable manpower or automation beyond our current capabilities to capture and invalidate or delete those posts. That is, a virus of harmful misinformation requires a valid and reliable test to identify it, an effective cure or quarantine, and a system to support that. It is not going to happen.

For SARS-CoV-2 while wider-testing and possible-vaccination exists only in our future, we have learned the demonstrably beneficial effects of social distancing. We do not know if we have it, we do not know who else has it, and we do not want it, so we maintain a distance of two metres, we stay at home, we wear masks, we do not touch our faces, we sneeze into our elbows. With any viral misinformation such as the 5G coronavirus conspiracy theory, its R0 is the speed and extent to which it is retweeted, shared and liked, and the only achievable way of reducing that is the social media equivalent of social distancing. It is easy to read a post, feel urged to share it as a result of genuine concern, outrage, disaffection, or identification and to just click to share it. Social media distancing would be any measure making that snap decision to share or retweet slower or more considered - for example, by requiring the user to re-enter their password, or to solve a Captcha, or to wait thirty seconds before the share button becomes active. The increased friction of such distancing would mitigate to some extent the casual, relatively thoughtless, or outrage-driven quick-shares, while continuing to allow anybody to share anything – only now in the context of just a moment’s thought. Importantly it would require no judgment on the part of the platforms as to what constituted dangerous, manipulative, or misleading information, with no problems of censorship, and no manpower. Nobody’s freedom of speech would be constrained. All that would be needed would be a simple redesign of the platform’s user interface. While weaponized troll-farms would continue in their efforts to subvert our lives by uploading polarizing and wrath-inducing posts on social media, those posts would survive just one posting-generation before hitting the mask and gown of the platforms’ social media distancing protocols. The R0 is reduced and social media gains a renaissance as a less divisive net good.

The platforms may balk at this. After all, our likes, retweets, shares and so on constitute data about us that can be monetized. However how much richer would be data derived from sharing actions borne of increased consideration, that we personally consider to be more valuable, compared to our current storm of relatively random clicks?

Social media distancing is the only workable solution to the pandemic of viral misinformation - Its cost minimal, but its benefit global.

[i] Riou J, Althaus CL (January 2020). "Pattern of early human-to-human transmission of Wuhan 2019 novel coronavirus (2019-nCoV), December 2019 to January 2020". Eurosurveillance. 25 (4). doi:10.2807/1560-7917.ES.2020.25.4.2000058. PMC 7001239. PMID 32019669.
[ii] https://twitter.com/NWOforum/status/1223870765893857281
[iii] https://www.theguardian.com/commentisfree/2020/apr/14/eamonn-holmes-5g-coronavirus
[iv] https://www.gov.uk/government/news/government-cracks-down-on-spread-of-false-coronavirus-information-online
[v] https://public.oed.com/updates/new-words-list-june-2005/

Social (Media) Distancing

Sent: 13 April 2020 11:53
To: 'info@eff.org' <info@eff.org>
Subject: Social (Media) Distancing

Hi

I don’t know who else to share this one thought with, so I hope you do not mind me sending it to EFF.

Simply – viral misinformation spreads due to it’s infectivity which, in the light of Covid-19 may as well be thought of as its R0. Social media might be asked to reduce the R0 by making it slightly harder to share/retweet/like any posts, for example by requiring the user’s password for each share/retweet/like.

This Social Media Distancing would be immediately implementable, and is separable from the technical and ethical complexities of censorship.

Thank you for everything that you do.

Jim Cromwell
UK

Regression Camper

An apparent trouble-shooter or consultant who arrives at an organisation during a downturn, hangs around making small changes until the organisation regresses back towards the mean, then leaves with another apparent success on their CV.

Information Theory and Privacy I (EFF)

This is a shameless cut and paste of the excellent EFF article here.

If we ask whether a fact about a person identifies that person, it turns out that the answer isn't simply yes or no. If all I know about a person is their ZIP code, I don't know who they are. If all I know is their date of birth, I don't know who they are. If all I know is their gender, I don't know who they are. But it turns out that if I know these three things about a person, I could probably deduce their identity! Each of the facts is partially identifying.

There is a mathematical quantity which allows us to measure how close a fact comes to revealing somebody's identity uniquely. That quantity is called entropy, and it's often measured in bits. Intuitively you can think of entropy being generalization of the number of different possibilities there are for a random variable: if there are two possibilities, there is 1 bit of entropy; if there are four possibilities, there are 2 bits of entropy, etc. Adding one more bit of entropy doubles the number of possibilities.1

Because there are around 7 billion humans on the planet, the identity of a random, unknown person contains just under 33 bits of entropy (two to the power of 33 is 8 billion). When we learn a new fact about a person, that fact reduces the entropy of their identity by a certain amount. There is a formula to say how much:

ΔS = - log2 Pr(X=x)

Where ΔS is the reduction in entropy, measured in bits,2 and Pr(X=x) is simply the probability that the fact would be true of a random person. Let's apply the formula to a few facts, just for fun:

Starsign: ΔS = - log2 Pr(STARSIGN=capricorn) = - log2 (1/12) = 3.58 bits of information
Birthday: ΔS = - log2 Pr(DOB=2nd of January) = -log2 (1/365) = 8.51 bits of information

Note that if you combine several facts together, you might not learn anything new; for instance, telling me someone's starsign doesn't tell me anything new if I already knew their birthday.3

In the examples above, each starsign and birthday was assumed to be equally likely.4 The calculation can also be applied to facts which have non-uniform likelihoods. For instance, the likelihood that an unknown person's ZIP code is 90210 (Beverley Hills, California) is different to the likelihood that their ZIP code would be 40203 (part of Louisville, Kentucky). As of 2007, there were 21,733 people living in the 90210 area, only 452 in 40203, and around 6.625 billion on the planet.

Knowing my ZIP code is 90210: ΔS = - log2 (21,733/6,625,000,000) = 18.21 bits
Knowing my ZIP code is 40203: ΔS = - log2 (452/6,625,000,000) = 23.81 bits
Knowing that I live in Moscow: ΔS = -log2 (10524400/6,625,000,000) = 9.30 bits

How much entropy is needed to identify someone?

As of 2007, identifying someone from the entire population of the planet required:

S = log2 (1/6625000000) = 32.6 bits of information.

Conservatively, we can round that up to 33 bits.

So for instance, if we know someone's birthday, and we know their ZIP code is 40203, we have 8.51 + 23.81 = 32.32 bits; that's almost, but perhaps not quite, enough to know who they are: there might be a couple of people who share those characteristics. Add in their gender, that's 33.32 bits, and we can probably say exactly who the person is.5

An Application To Web Browsers

Now, how would this paradigm apply to web browsers? It turns out that, in addition to the commonly discussed "identifying" characteristics of web browsers, like IP addresses and tracking cookies, there are more subtle differences between browsers that can be used to tell them apart.

One significant example is the User-Agent string, which contains the name, operating system and precise version number of the browser, and which is sent every web server you visit. A typical User Agent string looks something like this:

Mozilla/5.0 (Windows; U; Windows NT 5.1; en-GB; rv:1.8.1.6) Gecko/20070725 Firefox/2.0.0.6

As you can see, there's quite a lot of "stuff" in there. It turns out that that "stuff" is quite useful for telling different people apart on the net. In another post, we report that on average, User Agent strings contain about 10.5 bits of identifying information, meaning that if you pick a random person's browser, only one in 1,500 other Internet users will share their User Agent string.

EFF's Panopticlick project is a privacy research effort to measure how much identifying information is being conveyed by other browser characteristics. Visit Panopticlick to see how identifying your browser is, and to help us in our research.

  • 1.Entropy is actually a generalization of counting the number of possibilities, to account for the fact that some of the possibilities are more likely than others. You can find a pretty version of the formula here.

  • 2.This quantity is called the "self-information" or "surprisal" of the observation, because it is a measure of how "surprising" or unexpected the new piece of information is. It is really measured with respect to the random variable that is being observed (perhaps, a person's age or where they live), and a new, reduced, entropy for their identity can be calculated in the light of this observation.

  • 3.What happens when facts are combined depends on whether the facts are independent. For instance, if you know someone's birthday and gender, you have 8.51 + 1 = 9.51 bits of information about their identity because the probability distributions of birthday and gender are independent. But the same isn't true for birthdays and starsigns. If I know someone's birthday, then I already know their starsign, and being told their starsign doesn't increase my information at all. We want to calculate the change in conditional entropy of the person's identity on all the observed variables, and we can do that by making the probabilities for new facts conditional on all the facts we already know. Hence we see ΔS = -log2 Probability(Gender=Female|DOB=2nd of January) = -log2(1/2) = 1, and ΔS = -log2 Probability(Starsign=Capricorn|DOB=2nd of January)=-log2(1) = 0. In between cases are also possible: if I knew that someone was born in December, and then I learn that they are a Capricorn, I still gain some new bits of information, but not as much as I would have if I hadn't known their month of birth: ΔS = -log2 Probability(Starsign=Capricorn|month of birth=December)=-log2 (10/31) = 1.63 bits.

  • 4.Actually, in the birthday example, we should have accounted for the possibility that someone was born on the 29th of February during a leap year, in which case ΔS =-log2 Pr(1/365.25)

  • 5.If you're paying close attention, you might have said, "Hey, that doesn't sound right; sometimes there will be only one person in ZIP code 40203 who has a given birthday, in which case you don't need gender to identify them, and it's possible (but unlikely) that ten people in 40203 were all born on the 2nd of January. The correct way to formalize these issues would be to use the real fequency distribution of birthdays in the 40203 ZIP code.

Trivial Pursuit

So I couldn’t sleep…

In Trivial Pursuit there are Roll Again squares around the rim, but none up the spokes – so it is always a bad strategy to go up the spokes. But how much better is it? You can compare the probabilities of landing on the square you want from any square to work that out.

For the centre square that’s easy. No throw will get you back to the centre. Then from wherever you land there is a 1/6 probability of landing back on it. Job done.

For a pie slice you want it is more complicated… Let’s number the squares, with 0 being your target square (and where we will begin):

s-l1000.jpg

The board is symmetrical, so you can treat crossing a pie slice square the same as bouncing back from it – so for example four steps clockwise from square 2 returns you to square 2.

For simplicity, consider the non-target pie-slice to be a normal question.

Throw #0

t1.png

Your first throw from square 0, by itself, cannot get you back to square 0. It will only get you to the square with the same number as your dice-roll. From square 0, throws of 1, 3, 4, or 6 will end the run (that is, force you to answer a question). In my working they are red, for fail throws. A throw of 2 or 5 will give you a second throw. They are black, for still-in-play.

Let’s do the same thing for all the other squares, ie starting from square 1, 2, etc:

Throw #1

t2.png

Squares 2 and 5 are Roll Again.

A roll of 1 from square 1 gets you to the pie-slice-you-want-square. That is green for win. Likewise a roll of 2 from 2, 3 from 3 etc…

The colours indicate the outcomes of each possible throw from each possible square. Win, Continue, or Fail. There are two possible outcomes for each throw (clockwise and anticlockwise), but this diagram supposes you pick most strategically, preferring the pie-slice square to a Roll Again, and a Roll Again to a question.

This whole picture is just throw #1, from any square.

Ignoring square 0, there are 6 throws from six squares (36 outcomes)

14 fails (reds) = 14/36 = 7/18

16 continues (blacks) = 16/36 = 8/18 = 4/9

6 wins (greens) = 6/36 = 1/6

The black throws will only take you to square 2 or square 5. So the second throw can only be from square 2 or square 5…

Throw #2

t3.png

(The brown numbers are just the previous dice roll).

So a roll of 3 or 4 from square 1 on throw #1 gets you to square 2 or 5 respectively for throw two, and throw 2 outcomes are illustrated.

There are 96 possible outcomes for throw 2. However, the proportion of each outcome is the same for each starting square (the yellow or green highlighted ones). So it doesn’t matter how many sets of outcomes there are. There are:

3/6 fail (red) = 1/2

2/6 continue (black) = 1/3

1/6 win (green) = 1/6

 *** This is the same for throws 3, 4, 5, …. n. ***

Throw n

t4.png
 

The probability of winning on throw 1 =

The probability of winning on throw 2 =

The probability of winning on throw 3 =

The probability of winning on throw 4 =

The probability of winning on throw 5 =

The probability of winning on throw n =

 

P[1] =

P[2] =

P[3] =

P[4] =

P[5] =

P[n] =

 

1/6

4/9 x 1/6

4/9 x 1/3 x 1/6

4/9 x 1/3 x 1/3 x 1/6

4/9 x 1/3 x 1/3 x 1/3  x 1/6

4/9 x (1/3)^(n-2) x 1/6

= (2/27)*(1/3)^(n-2)

= 1/27 (see below)

Partial sum formula:

x1.gif

Decimal approximation: 0.037037037037037037

Convergence tests: By the geometric series test, the series converges.

Partial sum formula:

x2.gif

Partial Sums:

Throw 1 Onwards

The probability P of returning to your target-pie-slice-square, from is

P = P[1]+P[2]+…P[n]

P = 1/6 + (4/9 x 1/6) + 1/27

P = 5/18

So it’s 3/18 in throw 1, then an additional 2/18 for all throw combinations thereafter!

(And you should try to land on 3 or 4 if you can’t get your slice.)

Back to sleep…

The Revolution Will Be Live-Tweeted

You will not be able to log out, brother.
You will not be able to turn on, log in, and lurk.
You will not be able to lose yourself off-grid or
Block the ads from your feed,
Because the revolution will be live-tweeted.

The revolution will be live-tweeted.
The revolution will not be brought to you by credible
Unbiased or accountable journalists.
The revolution will not show you both sides
All sides or points in-between,
Nuance, uncertainty, clarity or fact.
Citations will be needed.
The revolution will be live-tweeted.

The revolution will be brought to you by
Algorithms grown from the regurgitated output
Of hate with traction, and outrage with likes.
The revolution will not gain the impressions you expect
The revolution will not respect your privacy
The revolution will re-tweet your lunch
Because the revolution will be live-tweeted, Brother.

There will be pictures of your face tagged by your friends
Which you can delete, if you can find that option,
But which will already have been used
To train AI’s, and to add to the 50,000
Datapoints that already identify you.
The revolution will be live-tweeted.

Do you accept the Terms and Conditions?
Scroll down for more.
Do you accept the Terms and Conditions?
Scroll down for more.
Click to accept the Terms and Conditions.
Click to submit your data in perpetuity.
Click to submit your friends’ data in perpetuity.
Click to subscribe in perpetuity.
The revolution will be supported by these razors,
By those beers, by that webhost.

The revolution will be controlled by
Four globally powerful organisations.
The revolution will be controlled by
Three globally powerful organisations.
The revolution will be controlled by
Two globally powerful organisations.
The revolution will be controlled by
One globally powerful organisation.
The revolution will be live-tweeted.

There will be no comments from users who are not
Paid-for, bad actors, or bot-farms.
The revolution will not sort by New.
The revolution will not respect your request to unsubscribe.
The revolution will deprecate your free subscription and
Bury your options behind forty clicks in pale text.
The revolution will continue in thirty seconds…

The revolution will be live-tweeted.
The revolution will be trending.
The revolution will distract you with in-app purchases.
The revolution will sell you things that you cannot own.
The revolution will not need your name to know who you are.
The revolution will know you better than you know yourself.
The revolution will own your industry with no assets.

The revolution will be live-tweeted, will be live-tweeted
will be live-tweeted, will be live-tweeted.
The revolution will be live-tweeted, Brothers.
The Revolution will be live.